Galactic-Scale Star Formation
Star Formation in Disk Galaxies
Stars form at widely varying rates in different disk galaxies (Kennicutt , 1998a). However, they appear to follow two simple empirical laws. The first is the correlation between the star formation rate density and the gas density D, the Schmidt law as first introduced by Schmidt (1959), SFR = A DN , (1) where SFR and D are the surface densities of star-formation rate (i.e. number of solar masses of gas that turn into stars per year and per kpc2 ) and gas (in solar masses per kpc2), respectively. When D and SFR are averaged over the entire star forming region of a galaxy, they give rise to a global Schmidt law. Kennicutt (1998b) found a universal global star formation law in a large sample that includes 61 normal spiral galaxies that have Halpha, HI and CO measurements and 36 infrared-selected starburst galaxies. The observations show that both the slope N ~ 1.3 - 1.5 and the normalization A appear to be remarkably consistent from galaxy to galaxy. There are some variations, though. For example, Wong & Blitz (2002) reported N ~ 1.1 - 1.7 for a sample of seven molecule-rich spiral galaxies, depending on the correction of the observed Halpha emission for extinction in deriving the star formation rate. Boissier et al. (2003) examined 16 spiral galaxies with published abundance gradients and found N ~ 2.0.
When D and SFR are measured radially within a galaxy, a local Schmidt law can be measured. Wong & Blitz (2002) investigated the local Schmidt laws of individual galaxies n their sample. They found similar correlations in these galaxies but the normalizations and slopes vary from galaxy to galaxy, with N ~ 1.2 - 2.1 for total gas, assuming that extinction depends on gas column density (or, N ~ 0.8 - 1.4 if extinction is assumed constant). Heyer et al. (2004) reported that M33 has a much deeper slope, N ~ 3.3. The second empirical law is the star formation threshold. Stars are observed to form efficiently only above a critical gas surface density. Martin & Kennicutt (2001) studied a sample of 32 nearby spiral galaxies with well-measured Halpha and H2 profiles, and demonstrated clear surface-density thresholds in the star formation laws in these galaxies. They found that the threshold gas density (measured at the outer threshold radius where SFR drops sharply) ranges from 0.7 to 40 Msun/pc2 among spiral galaxies, and the threshold density for molecular gas is ~ 5 - 10 Msun/pc2. However, they found that the ratio of gas surface density at the threshold to the critical density for Toomre (1964) gravitational instability is remarkably uniform. They assumed a constant velocity dispersion of the gas, the effective sound speed, of cs = 6 km/s. Such a density threshold applies to normal disk galaxies (e.g., Boissier et al. 2003), elliptical galaxies (e.g., Vader & Vigroux 1991), low surface brightness galaxies (van der Hulst et al., 1993), and starburst galaxies (Elmegreen, 1994). However, there are a few exceptions, such as dwarf and irregular galaxies (e.g., Hunter, Elmegreen & Baker 1998). Furthermore, inefficient star formation can be found well outside the threshold radius (Ferguson et al., 1998).
What is the origin of the Schmidt laws and the star formation thresholds? The mechanisms that control star formation in galaxies, such as gravitational instability, supersonic turbulence, magnetic fields, and rotational shear are widely debated (Shu et al. 1987; Elmegreen 2002; Larson 2003; Mac Low & Klessen 2004). The first model emphasizes self-gravity of the galactic disk (e.g., Larson 1988; Kennicutt 1989; Elmegreen 1994; Kennicutt 1998b). In this model, the Schmidt laws do not depend on the local star formation process, but are simply the results of global gravitational collapse on a free-fall time. In the second model, the global star formation rate scales with either the local dynamical time, invoking cloud-cloud collisions (e.g. Wyse 1986; Wyse & Silk 1987; Silk 1997; Tan 2000), or the local orbital time of the galactic disk (e.g. Elmegreen 1997; Hunter et al. 1998). A third model, which invokes hierarchical star formation triggered by turbulence, has been proposed by Elmegreen (2002). In this model, the Schmidt law is scale-free, and the star formation rate depends on the probability distribution function (PDF) of the gas density produced by galactic turbulence, which appears to be log-normal in several simulations of turbulent molecular clouds and ISM (e.g., Scalo et al. 1998; Passot & Vázquez-Semadeni 1998; Ostriker, Gammie, & Stone 1999; Klessen 2000; Wada & Norman 2001; Ballesteros-Paredes & Mac Low 2002; Padoan & Nordlund 2002; Li, Klessen, & Mac Low 2003; Kravtsov 2003; Mac Low et al. 2005). Recently, Krumholz & McKee (2005) extended this analysis with additional assumptions such as the virialization of the molecular clouds and star formation efficiency to derive the star formation rate from the gas density PDFs. They successfully fitted the global Schmidt law, but their theory still contains several free or poorly constrained parameters, and does not address the observed variation in local Schmidt laws among galaxies.
Numerical Studies in the Group
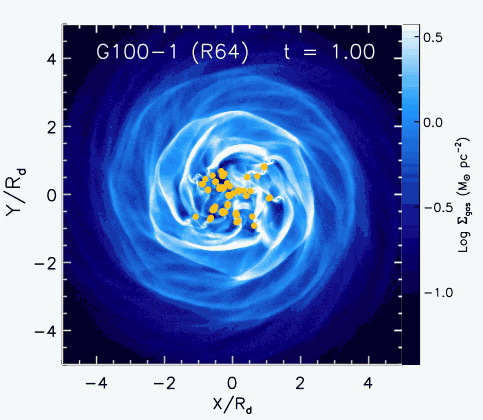
In Li et al. (2005a,b, 2006) we reported results of gas dynamical models of star formation at the galactic scale. We used the smoothed particle hydrodynamics (SPH) code GADGET, v1.1 (Springel, Yoshida & White, 2001), modified to include absorbing sink particles (Bate, Bonnell & Price, 1995) to directly measure the mass of gravitationally collapsing gas. Li et al. (2005b) and Jappsen et al. (2005) give detailed descriptions of sink particle implementation and interpretation. In short, a sink particle is created from the gravitationally bound region at the stagnation point of a converging flow where number density exceeds values of n = 103 cm-3. It interacts gravitationally and inherits the mass, and linear and angular momentum of the gas. It accretes surrounding gas particles that pass within its accretion radius and are gravitationally bound.
Regions where sink particles form have pressures P /k ~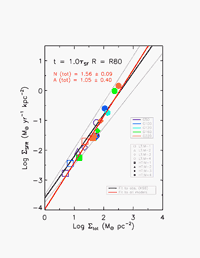 107 K/cm3 typical of massive star-forming regions. The only regions that reach these high pressures in our simulations are dynamically collapsing. The measured mass of the collapsing gas is insensitive to the value of the cutoff density. This is not an important free parameter for us, unlike in the models of Elmegreen (2002) and Krumholz & McKee (2005). Our galaxy model is as simple as possible to provide physical clarity. We use a dark matter halo, and a disk of stars and isothermal gas, but neglect bulges in most cases. The initial galaxy structure is based on the analytical work of Mo, Mao & White (1998), as implemented numerically by Springel & White (1999); Springel (2000) and Springel, Di Matteo & Hernquist (2005). We characterize our models by the rotational velocity V200 at the virial radius R200 where the density reaches 200 times the cosmic average. We have run models of galaxies with rotational velocity V200 = 50 - 220 km/s, with gas fractions of 20 - 90% of the disk mass for each velocity.
107 K/cm3 typical of massive star-forming regions. The only regions that reach these high pressures in our simulations are dynamically collapsing. The measured mass of the collapsing gas is insensitive to the value of the cutoff density. This is not an important free parameter for us, unlike in the models of Elmegreen (2002) and Krumholz & McKee (2005). Our galaxy model is as simple as possible to provide physical clarity. We use a dark matter halo, and a disk of stars and isothermal gas, but neglect bulges in most cases. The initial galaxy structure is based on the analytical work of Mo, Mao & White (1998), as implemented numerically by Springel & White (1999); Springel (2000) and Springel, Di Matteo & Hernquist (2005). We characterize our models by the rotational velocity V200 at the virial radius R200 where the density reaches 200 times the cosmic average. We have run models of galaxies with rotational velocity V200 = 50 - 220 km/s, with gas fractions of 20 - 90% of the disk mass for each velocity.
With the sink particle technique the total collapse rate in our galaxies can be measured at any time, allowing us to derive a quantity related to the star formation rate, and compare it to the gas surface density. Our models fit the observed relation in both slope and normalization. In this plot, we used a constant conversion factor between collapse rate and star formation rate of 30% (a local efficiency for star formation in very unstable regions), but Li et al. (2006) demonstrate that local efficiencies within a reasonable range (i.e. 5 - 50%) give similar results.
Responsible: , last modification Jan/31/2008 11:12 CET